Площадь поверхности - это суммарная площадь всех внешних сторон трехмерного объекта. Рассмотрим методы расчета для различных геометрических фигур.
Содержание
Основные формулы для расчета площади поверхности
| Фигура | Формула | Обозначения |
| Куб | S = 6a² | a - длина ребра |
| Прямоугольный параллелепипед | S = 2(ab + bc + ac) | a, b, c - длины ребер |
| Цилиндр | S = 2πr(h + r) | r - радиус, h - высота |
| Сфера | S = 4πr² | r - радиус |
| Конус | S = πr(r + l) | r - радиус, l - образующая |
Пошаговый алгоритм расчета
- Определите тип геометрической фигуры
- Измерьте необходимые параметры (длины, радиусы)
- Выберите соответствующую формулу
- Подставьте значения в формулу
- Выполните вычисления
- Проверьте единицы измерения
Пример расчета для куба
- Длина ребра (a) = 5 см
- Формула: S = 6a²
- Вычисление: 6 × (5 см)² = 6 × 25 см² = 150 см²
Особые случаи расчета
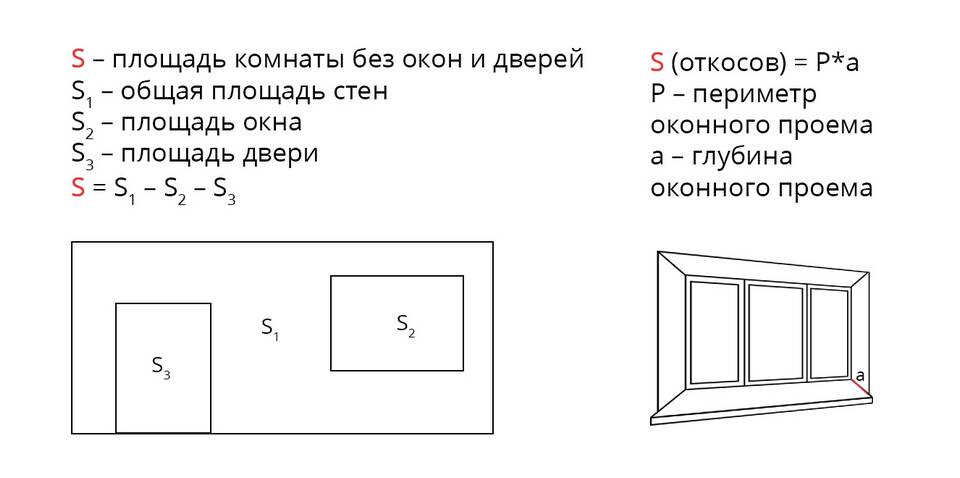
Составные фигуры
Для фигур, состоящих из нескольких простых элементов:
- Разбейте объект на простые составляющие
- Вычислите площадь каждой части
- Сложите полученные значения
- Вычтите площади соприкасающихся поверхностей
Неправильные формы
Для объектов сложной формы:
- Используйте метод триангуляции
- Примените интегральное исчисление
- Используйте специализированное ПО для 3D-моделирования
Практическое применение
| Область | Применение |
| Строительство | Расчет материалов для отделки |
| Производство | Определение расхода покрытий |
| Дизайн | Планирование пространства |
| Наука | Физические и химические расчеты |
Важные замечания
- Все измерения должны быть в одинаковых единицах
- Для точных расчетов используйте значение π с достаточным количеством знаков
- При работе с реальными объектами учитывайте неровности поверхности
- Проверяйте правильность формулы для конкретной фигуры