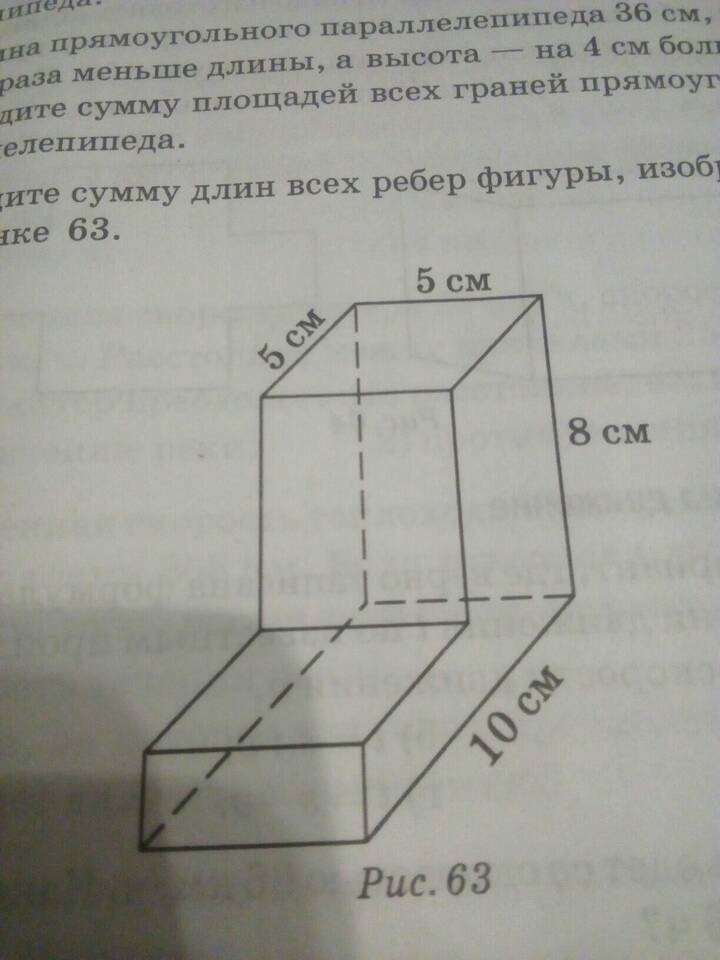
Сумма длин представляет собой математическую операцию сложения значений длин отрезков, сторон фигур или других линейных измерений. Рассмотрим основные методы вычисления суммы длин в различных геометрических задачах.
Содержание
Основные понятия и формулы
Для вычисления суммы длин необходимо знать:
- Единицы измерения длины (метры, сантиметры, миллиметры)
- Свойства геометрических фигур
- Формулы периметров различных фигур
- Принципы сложения величин
Формулы периметров фигур
| Фигура | Формула суммы длин |
| Квадрат | P = 4 × a |
| Прямоугольник | P = 2 × (a + b) |
| Треугольник | P = a + b + c |
| Окружность | C = 2πr |
Пошаговый алгоритм вычисления
Для простых отрезков
- Измерьте длину каждого отрезка
- Убедитесь, что все значения в одинаковых единицах
- Сложите все полученные значения
- Запишите результат с указанием единиц измерения
Для сложных фигур
- Разбейте фигуру на простые элементы
- Найдите длину каждого элемента
- Сложите длины всех элементов
- Учтите возможные повторяющиеся участки
Практические примеры
Пример 1: Сумма длин сторон многоугольника
Дано: пятиугольник со сторонами 5 см, 7 см, 4 см, 6 см, 8 см
Решение: 5 + 7 + 4 + 6 + 8 = 30 см
Пример 2: Периметр прямоугольника
Дано: длина = 12 м, ширина = 5 м
Решение: 2 × (12 + 5) = 34 м
Особые случаи
- При наличии дробных значений - сложение дробей
- При разных единицах измерения - приведение к одной системе
- Для криволинейных фигур - использование специальных формул
- В трехмерных объектах - вычисление суммы ребер
Таблица перевода единиц
| Единица | В метрах |
| 1 километр | 1000 м |
| 1 сантиметр | 0,01 м |
| 1 миллиметр | 0,001 м |
Проверка правильности вычислений
- Повторите вычисления другим способом
- Оцените правдоподобность результата
- Используйте калькулятор для проверки
- Сравните с аналогичными известными примерами